Introduction
Apprendre les maths, ce n’est pas juste une question d’intelligence ou de chance. C’est surtout une question de méthode. Certaines approches sont beaucoup plus efficaces que d’autres pour assimiler les notions, mémoriser les formules et réussir ses exercices.
Dans cet article, je te partage les 5 méthodes d’apprentissage les plus utilisées et reconnues par les enseignants, les coachs pédagogiques et les étudiants performants. À toi de trouver celle qui te correspond le mieux… ou de les combiner intelligemment !
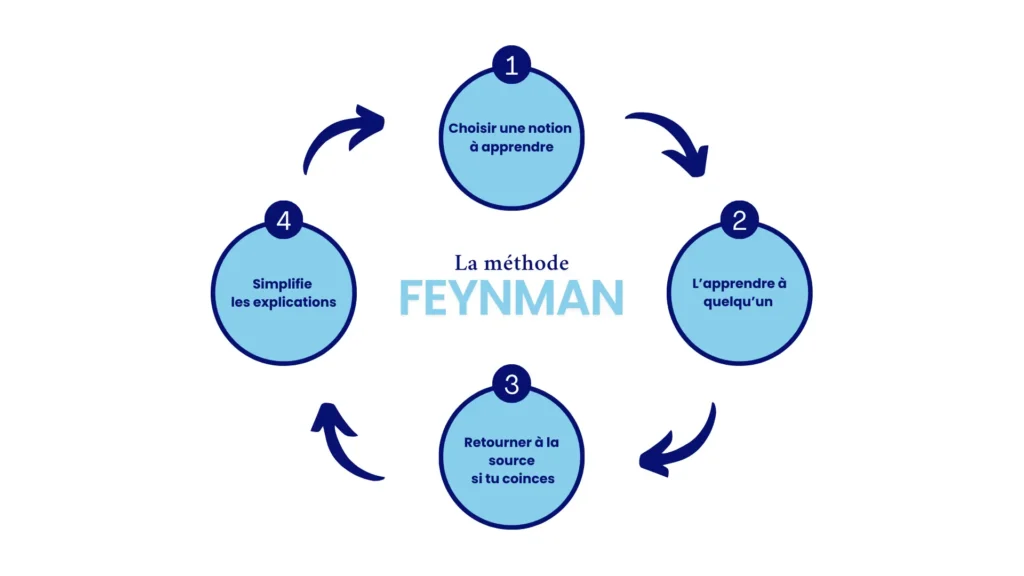
1. ???? La méthode active (ou méthode Feynman)
“Si tu ne peux pas l’expliquer simplement, c’est que tu ne l’as pas bien compris.” – Richard Feynman
Cette méthode consiste à réexpliquer la notion avec tes propres mots, comme si tu devais l’enseigner à un camarade.
Tu identifies ensuite les zones floues, tu les retravailles, et tu recommences.
???? Idéal pour : approfondir sa compréhension, détecter ses lacunes.
???? Outils recommandés : tableau blanc, feuilles volantes, enregistrement vocal.
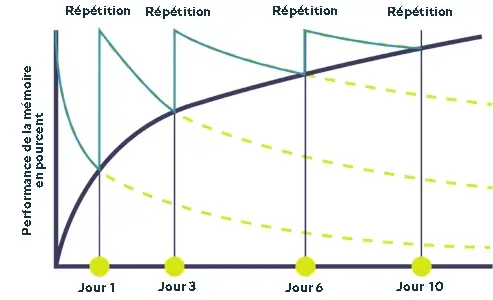
2. ???? La répétition espacée (Spaced Repetition)
C’est une des techniques les plus puissantes pour mémoriser durablement. Elle repose sur le fait que l’on retient mieux quand on revoit les infos au bon moment, juste avant de les oublier.
???? Il existe des applis comme Anki ou Quizlet qui t’aident à planifier automatiquement les révisions.
???? Idéal pour : apprendre les formules, les définitions, les démonstrations types.
???? Outils recommandés : flashcards papier ou numériques, appli de révision.
3. ✍️ La pratique intensive (Learning by Doing)
Rien ne vaut la pratique. En maths, plus tu fais d’exercices, plus tu comprends les mécanismes, plus tu développes des réflexes.
Le but n’est pas de faire 100 exos d’affilée, mais de varier : facile, moyen, difficile, puis retour sur les erreurs.
???? Idéal pour : automatiser les raisonnements, prendre confiance.
???? Outils recommandés : manuels scolaires, plateformes d’exercices interactifs, sujets d’annales.

4. ???? L’apprentissage multimodal (visuel, auditif, kinesthésique)
Chacun a sa façon d’apprendre. Certains ont besoin de voir (schémas, couleurs), d’autres de faire (manipuler, tracer), ou d’écouter (vidéos, explications à voix haute).
???? Le vrai plus, c’est de mixer les canaux pour renforcer ta mémorisation. Regarde une vidéo + résume sur papier + refais les exercices.
???? Idéal pour : ceux qui n’accrochent pas aux méthodes classiques.
???? Outils recommandés : YouTube, cartes mentales, podcasts, vidéos de cours.

5. ????♂️ La métacognition : apprendre à apprendre
C’est LA méthode des élèves qui réussissent. Il s’agit de prendre du recul sur sa façon d’apprendre :
- Qu’est-ce qui a marché pour moi aujourd’hui ?
- Qu’est-ce que je peux améliorer demain ?
- Est-ce que je comprends vraiment ou je récite mécaniquement ?
???? Idéal pour : les élèves autonomes ou qui veulent le devenir.
???? Outils recommandés : journal d’apprentissage, auto-évaluation, rétroactions régulières.

???? Conclusion
Il n’y a pas une seule bonne méthode pour apprendre les maths. L’idée, c’est d’expérimenter, de mélanger ce qui marche pour toi, et de rester régulier dans tes efforts.
Et surtout : n’oublie pas que les maths, c’est comme un sport, plus tu t’entraînes intelligemment, plus tu gagnes en aisance.
| Méthode | Idéal pour… | Outil recommandé |
| Méthode Feynman | Comprendre en profondeur | Tableau blanc, vocal |
| Répétition espacée | Mémoriser durablement | Anki, flashcards |
| Pratique intensive | Automatiser les réflexes | Exercices + corrigés |
| Multimodal | Stimuler plusieurs sens | Vidéos, couelurs, schémas |
| Métacognition | Apprendre à apprendre | Journal de bord |





Laisser un commentaire